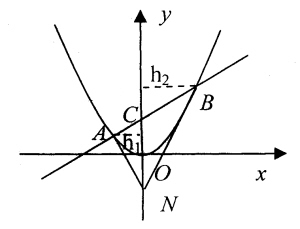
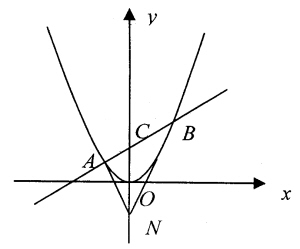
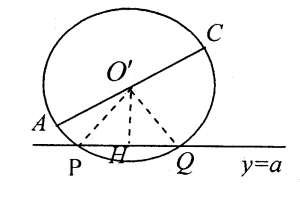
1. 在平面直角坐标系xOy中，过定点C(0，P)作直线与抛物线x2=2py(p>0)相交于A，B两点。

(Ⅰ)若点N是点C关于坐标原点O的对称点，求△ANB面积的最小值；

(Ⅱ)是否存在垂直于y轴的直线l，使得l被以AC为直径的圆截得的弦长恒为定值？若存在，求出l的方程；若不存在，说明理由(此题不要求在答题卡上画图)。

解：(1)过C点的直线y=kx+p，k存在。A(x1，y1)、B(x2，y2)

-x2-2pkx-2p2=0

△=4p2k2+8p2>0

x1+x2=2pk，x1x2=-2p2

如右图：

S△ANB=S△ANC+S△BNC

=-|NC|gh1+-|NC|gh2

=-|NC|g(h1+h2)

=-·2pg|x2-x1|=p|x2-x1|

|x2-x1|2

=(x1+x2)2-4x1x2

=4p2g(k2+2)

∴S△ANB=2p2g-

∴当k=0时，

(S△ANB)min=2-p2

分析：(2)如右示意图A(x1，y1)、C(0，p)、O'(-，-)

R=|O'p|=-|AC|

=--

=--

=--

|O'H|=|--a|

=-|y1+p-2a|

|PH|2=|O'P|2-|O'H|2

=-[(y12+p2)-(y1+p-2a)2]

=y1(a--)+a(p-a)

分析上面的式子，A为抛物线上的动点，所以y1是变量，p为常量，a为所求，定值是与变量y1无关的值，即在解析式中消去y1。

由此，设a=-，|PH|2=-，|PH|=-

|PQ|=2|PH|=p(定值)

注：(2)是定值问题的分析方法，要分清常量与变量及变量与所求量。

2. 已知椭圆C的中心在坐标原点，焦点在x轴上，椭圆C上的点到焦点距离的最大值为3；最小值为1。

(Ⅰ)求椭圆C的标准方程；

(Ⅱ)若直线l，y=kx+m与椭圆C相交于A，B两点(A，B不是左右顶点)，且以AB为直径的圆过椭圆C的右顶点。求证：直线l过定点，并求出该定点的坐标。

解(1)

-

∴-+-=1

分析(2)-

→(4k2+3)x2+8kmx+4(m2-3)=0

△=64m2k2-16(4k2+3)(m2-3)>0

→3+4k2-m2>0

A(x1，y1)、B(x2，y2)，D(2，0)

x1+x2=--

x1·x2=-

由几何条件：AB为直径的圆过点D，∴|AD|⊥|BD|

∴kAD·kBD=-1

-=-1

y1·y2=(kx1+m)·（kx2+m)

=k2x1x2+km(x1+x2)+m2

=-

y1y2+x1x2-2(x1+x2)+4=0

-+-+-+4=0

(7m+2k)(m+2k)=0，这里m，k均为变量，要求l过定点，只有把m，k代入原方程，m1=--k，m2=-2k

当l:y=kx--k=k(x--)，若，l需与k无关，∴x=-，y=0，定点为(-，0)。

当l:y=kx-2k=k(x-2)，l过点D不合题意.

注：本题(2)是直线与椭圆相交的基本类型，对直线的要求是过定点。